Распознаем покерные фишки
Обычно статьи про компьютерное зрение рассказывают о распознавании лиц и автомобильных номеров. Но мало кто знает, что эту технологию используют в казино для сбора статистики. Игровой стол записывают на видео, считывают карты и ставки игроков.
В этой статье рассмотрим подход к распознаванию покерных фишек. Приведенный алгоритм применим как для изображений, так и для видео. Реализовать этот подход можно, например, с помощью OpenCV, в котором уже присутствуют стандартные алгоритмы.
Что будем делать
Необходимо найти стопку покерных фишек и определить ее стоимость.
Покерный стол и фишки будем рассматривать такие, как на скриншоте ниже.

Рисунок 1: Покерный стол
При этом считаем, что камера закреплена и стоит всегда в одинаковом месте. Это условие используем лишь для того, чтобы выделить на покерном столе небольшие сегменты, в которых ищем фишки. Эти сегменты будем использовать как исходные данные.

Рисунок 2: Исходные данные. Первый образец

Рисунок 3: Исходные данные. Второй образец
Считаем также, что камера выровнена горизонтально, то есть стопка фишек почти вертикальная. Также допустим, что стопка выглядит как цилиндр, без вылезающих фишек. Все фишки имеют одинаковую толщину.
Стираем задний план
Прежде всего отфильтруем стол от стопки фишек. Для этого подойдет сегментация изображения методом GrabCut.
При этом нам будут мешать узоры на столе (желтоватая окружность). Их можно легко убрать с изображения, заменив все цвета близкие к желтому на черный.

Рисунок 4: Фильтрация узоров. Первый образец

Рисунок 5: Фильтрация узоров. Второй образец
Затем воспользуемся сегментацией изображения.

Рисунок 6: Без заднего плана. Первый образец

Рисунок 7: Без заднего плана. Второй образец
Ищем верхушку стопки
Чтобы отыскать количество фишек в стопке, нам придется отыскать какие-то характерные детали на изображении. Первое, что приходит в голову - это разделительные линии между фишками. Но они не ярко выраженные, и на некоторых изображениях не видны. Однако, даже в этом случае мы легко скажем, сколько фишек в стопке. Работу глазу облегчают белые маркеры, нанесенные на боковую часть каждой фишки, вероятно, именно с этой целью.
На первый взгляд отыскать маркеры не составляет труда - ведь они белые, а значит состоят из самых ярких точек изображения. Но это не так, таковыми являются только маркеры на верхушке стопки, потому что они хорошо освещены. На боковую часть стопки свет падает под углом и поэтому яркость у боковых маркеров небольшая.
Это сыграет нам на руку, потому что мы сможем отыскать 6 маркеров с верхушки стопки. Для этого переведем изображение в градации серого и возьмем порог с довольно большим значением. Потом найдем контуры полученных объектов и отфильтруем их по размеру.
В итоге получим изображение, на котором есть по крайней мере 5 маркеров с крышки стопки. Ниже показаны изображения, растянутые по вертикали для наглядности.

Рисунок 8: Белые маркеры с верхушки стопки. Первый образец

Рисунок 9: Белые маркеры с верхушки стопки. Второй образец
О проблемах с формой фишки
Найти количество фишек было бы гораздо проще, если бы стопка имела прямоугольную форму вместо проекции цилиндра. Попробуем это исправить.
Можно попробовать обратить проекцию, но тогда придется учитывать углы камеры, которые нам неизвестены. Есть способ получше. Он основан на том, что нет нужды обращать проекцию полностью. Достаточно лишь вернуть контурам прямоугольный вид. Внутренность фишек - почти монотонный цвет, деформации этих областей не добавят никаких искажений.
Найдем эллипс - границу верхушки стопки. Граница каждой фишки совпадает с сегментом этого эллипса. Поднимем каждую полоску изображения шириной в 1 пиксел на то значение, которое является “ординатой уравнения эллипса”.
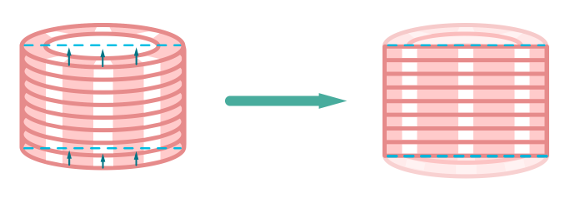
Рисунок 10: Схема выправления стопки фишек.
Ищем эллипс
Как найти уравнение этого заветного эллипса? Его можно провести через известные маркеры с верхушки стопки. Но найденные маркеры представляют собой контуры и необходимо выбрать на каждом контуре одну точку, которая будет представлять этот маркер.
Найдем самую “удаленную” точку на контуре маркера. Расстояние от центра эллипса до этой точки максимально. Возьмем центр масс системы из всех контуров маркеров (это предполагаемый центр эллипса) и выберем из каждого контура маркеров самую удаленную от этого центра точку.

Рисунок 11: Самые удаленные точки контуров маркеров. Первый образец

Рисунок 12: Самый удаленные точки контуров маркеров. Второй образец
На рисунке выше изображены только 5 точек, потому что ровно столько необходимо для построения эллипса. Разберемся почему.
Интерполировать эллипс можно разными способами. Один из них состоит в использовании уравнения эллипса в виде квадратичной формы, а другой в виде уравнения:
(x / a) ^ 2 + (y / b) ^ 2 = 1
В первом случае будут линейные уравнения, что проще, но затем придется вычислять собственные числа у матриц, что приведет к использованию численных методов. Во втором случае будут нелинейные уравнения. Таким образом в любом случае придется воспользоваться приближенными вычислениями, поэтому выберем второй способ.
Чтобы найти эллипс мы подставим все известные точки эллипса в общее уравнение эллипса. Получим систему из некоторого количества уравнений вида:
(x_i / a) ^ 2 + (y_i / b) ^ 2 = 1
где x_i, y_i - координаты известной i-ой точки на эллипсе.
Сколько необходимо взять точек? Столько же сколько и неизвестных, тогда количество уравнений и количество неизвестных совпадут и система сможет иметь однозначное решение. На деле она всегда будет иметь решение, так как мы знаем, что искомый эллипс существует (он нарисован на изображении). Если же решения нет, то это означает, что положения маркеров найдены неверно.
Итак, количество неизвестных две - a и b. Но это лишь потому, что мы взяли уравнение эллипса проходящего через начало координат. Добавим сдвиг на x0, y0:
x = x` + x0
y = y` + y0
и подставим в уравнение эллипса. Получим эллипс, центр, которого уже может располагаться где угодно. Теперь количество неизвестных четыре. Но и этого будет недостаточно. Камера не всегда расположена удачно, она выровнена так, что оси эллипса лишь приблизительно параллельны осям координат. Поэтому добавим поворот на угол alpha:
x` = x`` * cos(alpha) - y`` * sin(alpha)
y` = x`` * sin(alpha) + y`` * cos(alpha)
и подставим в уравнение эллипса со сдвигом. Получим эллипс наиболее общего вида. Неизвестных теперь 5 - a, b, x0, y0, alpha. Для их поиска потребуется знать 5 точек на эллипсе, поэтому 5 маркеров нам будет ровно в самый раз.
Нелинейную систему из 5 уравнений можно решить, например, методом Ньютона. Точность вычислений для x0, y0, a, b ограничивается 1 пикселем, а для угла alpha точность следует подобрать. Начальное приближение выбрать совсем несложно: для x0, y0 - это найденный ранее центр масс системы маркеров, для alpha - это 0, так как угол считается малым (камера стоит почти ровно), радиусы a, b - можно найти из прямоугольника, который описывает систему из 5 маркеров.

Рисунок 13: Найденный эллипс. Первый образец

Рисунок 14: Найденный эллипс. Второй образец
Выпрямляем стопку
Имея на руках уравнение эллипса верхушки стопки можно получить изображение фишек “без искажений”. Для этого следует разбить изображение на вертикальные полосы шириной в 1 пиксел и каждую полосу сдвинуть вверх на нижнюю ординату эллипса.

Рисунок 15: Схема выправления стопки фишек.
Таким образом, нижняя часть эллипса превратится в прямую линию, а изображение фишек превратится в набор горизонтальных прямоугольников.

Рисунок 16: Выправленная стопка фишек. Первый образец

Рисунок 17: Выправленная стопка фишек. Второй образец
Как видно из рисунков, выправление происходит не так гладко, даже несмотря на то, что эллипс найден довольно точно. Результат зависит от того, насколько малы углы камеры и насколько стопка отличается по форме от цилиндра. Также можно видеть, что левая и правая части изображения выправлены довольно грубо, в то время как центральная часть - приемлемо. Это неудивительно, потому что именно по краям стопка была наиболее искривлена.
Дальше будем использовать только центральную часть найденного изображения, шириной примерно в треть.
Ищем высоту одной фишки
Дальнейшее распознавание кажется простым, однако здесь есть проблема - необходимо отыскать высоту одной фишки.
Если в стопке есть цвет, у которого только одна фишка, то отыскать размер фишки не представляет труда. Для этого нужно разбить изображение на сегменты по цвету. Затем вычислить высоту каждого сегмента. Минимальная из них будет высотой одной фишки.
Можно улучшить точность этого метода, если учесть, что высота фишки всегда делит высоту изображения (то есть отношение второго к первому есть целое число), потому что изображение состоит только из фишек, и все они имеют одинаковую толщину. Пусть h0 - вычисленная высота одной фишки, а H - высота изображения, тогда количество фишек C и уточненная высота одной фишки h1 равны:
C = round(H / h0)
h1 = H / C
Тем не менее, условие, что в стопке всегда есть обособленная фишка слишком сильное. Избавиться от него, можно с помощью все тех же маркеров. В самом деле, эти маркеры были нанесены на фишки с целью облегчить работу глазу, а значит могут облегчить и распознавание.
Здесь тоже есть свои ограничения.
Маркеры могут находиться строго друг под другом, а тогда две фишки склеются для компьютера.
Вероятность такого события не столь велика.
Если рассматривать “строго друг под другом” так, что абсциссы маркеров у двух фишек совпадают, то вероятность равна нулю.
На практике это ограничение будет означать, что абсциссы маркеров двух фишек отличаются менее, чем на 1 пиксел.
Поэтому вероятность такой коллизии, будет равна 3 / W, где W - ширина изображения.
Это так, потому что по периметру фишки находятся 6 маркеров, а камера видит примерно половину периметра фишки, то есть из всех абсцисс “удачными” для коллизии, будут только 3. При W=300 вероятность коллизии равна 1%.
А вероятность P10 того, что в стопке из 10 фишек будет хотя бы одна коллизия:
P10 = 1 - (1 - p)^9 = 1 - (1 - 0.01)^9 = 0.086
то есть 8.6%.
Для приемлемого алгоритма не стоит накладывать больше никаких дополнительных ограничений.
Найдем для каждого маркера его левую границу. Для этого вычислим горизонтальный градиент черно-белого изображения. Левые границы маркеров практически строго вертикальные, поэтому они будут присутствовать на градиенте. Однако также там будут и правые границы. Если же взять только положительные значения градиента, то на изображении останутся только левые границы, так как на правых границах яркость изображения падает (с яркого маркера на темную фишку). На рисунке ниже показан возможный результат.

Рисунок 18: Левые границы маркеров. Первый образец

Рисунок 19: Левые границы маркеров. Второй образец
В идеале все высоты найденных контуров должны совпадать и равняться высоте одной фишки. Как видно из рисунка это не так. Возьмем за высоту фишки медианное среднее из всех высот контуров. Это даст хороший результат в предположении, что большинство найденных контуров практически точные, а случайно испортившихся контуров мало.
Медианое среднее даст хороший результат только в том случае, если левые границы маркеров нигде не склеются в одну большую, а это, как было вычислено ранее, случается не так уж редко. В этом случае перед тем, как вычислять среднее, оставим только те контуры, которые удовлятворяют такому условию:
min_height < h < Z * min_height
1 < Z < 2
где min_height - минимальная высота всех контуров, h - высота допустимого контура, Z - коэффициент допустимости. Суть условия в том, что высоты контуров хоть и могут отличаться, но не настолько сильно, как отличается высота одной фишки от высоты двух.
Каким выбрать коэффициент Z? Не стоит брать его равным 2, так как высота двух фишек тоже неточная и может варьироваться (то есть может оказаться меньше чем 2 * min_height).
Если выбрать “наименьшее из двух зол” - 1.5, то результат получается неплохой.
Можно немного уточнить Z, исходя из эвристического соображения, что если высота одной фишки может отличаться на w, то высота двух фишек отличается на 2*w, поэтому соотношение “двух зол” не 1:1, а 1:2. То есть Z = 1.33.
В итоге, чтобы найти высоту одной фишки необходимо:
- Найти левые границы маркеров с помощью горизонтального градиента
- Отфильтровать границы по размеру (чтобы не сильно отличались по высоте от минимальной)
- Найти медианое среднее высот границ
- Улучшить полученное значение с учетом того, что высота фишки делит высоту стопки
Определяем цвета фишек
На данном этапе имеем изображение стопки фишек в виде горизонтальных прямоугольников. Высота каждого прямоугольника одинакова и известна. Значит можно разбить изображение на n горизонтальных полосок, где n - количество фишек в стопке.
Если для каждой полоски найти цвет, то можно будет сказать сколько фишек определенного цвета в стопке.
Пусть палитра цветов фишек состоит из 5 цветов - красный, синий, зеленый, черный и белый (таковы цвета фишек из тестовых образцов). Необходимо определить цвет полоски из палитры. Для этого достаточно найти “средний” цвет полоски и найти ближайший к нему цвет из 5-ти предложенных. Чтобы это формализовать, придется определить понятие среднего цвета и определить расстояние между цветами (ввести метрику).
Средний цвет можно легко вычислить, если взять среднее арифметическое rgb-компонент цветов. Но здесь, как и на этапе вычисления высоты фишки больше подойдет медианное среднее, так как точек с полезными цветами много, а цветовой “шум” может быть большим по величине. Но как вычислить медианное среднее? Ведь для этого необходимо сначала отсортировать цвета, а они представляются векторами.
Отложим вопрос о среднем. Как ввести расстояние между цветами? В понятии расстояния должна содержаться информация о том, как мы различаем фишки. Если две одинаковые фишки освещены по-разному их все равно признают за одну и ту же фишку. Поэтому яркость цвета в этом вопросе не важна, а значит удобно рассмотреть представление цвета в виде HSV (упрощенно - оттенок, насыщенность, яркость). Насыщенность тоже не сильно влияет на цвет фишки - едва ли встречаются фишки бледно-красного и ярко-красного цветов. Заметить различие между цветами гораздо проще, если они имеют разные оттенки. В самом деле, цвета из палитры очень сильно отличаются по оттенку (красный, синий, зеленый). В фишках другой расскраски бывают еще желтые и фиолетовые цвета. Таким образом, наилучшее расстояние для цветов фишек - это разность оттенков.
Однако, оттенок не определен у черного и белого цветов. Более того, монохроматические (градации серого) цвета следует сравнивать по яркости. Таким образом метрика для немонохроматических цветов p1 это разность оттенков, а для монохраматических p2 - это разность яркостей.
p1(x, y) = |x.hue - y.hue|
p2(x, y) = |x.value - y.value|
где x, y - цвета, а hue, value - их оттенок и яркость соответственно.
Таким образом, сначала следует определить является ли фишка цветной или черно-белой. Затем, необходимо оставить в рассмотрении только те точки изображения, которые обладают такой же “цветностью” как и фишка. В первом случае характеристикой цвета для нас будет оттенок, во втором - яркость. Для этих характеристик медианное среднее вычисляется обычным образом, а расстояние введено выше (тоже обычным образом). Вычислив средний цвет фишки, можно найти максимально приближенный к нему цвет из палитры.
Остался вопрос - как определить является ли фишка цветной? По значению насыщенности. Можно подобрать порог насыщенности, выше которого будем считать фишку цветной, а ниже - черно-белой.

Рисунок 20: Фишки с цветами. Слева - горизонтальные полоски, справа - вычисленные по изображению цвета. Первый образец

Рисунок 21: Фишки с цветами. Слева - горизонтальные полоски, справа - вычисленные по изображению цвета. Второй образец
Результат
Резюмируя, для того чтобы распознать фишки и их цвета, мы проделали следующие этапы:
- Удалить фон на изображении
- Найти эллипс верхушки стека по белым маркерам
- Убрать кривизну стека
- Найти высоту одной фишки по белым маркерам
- Определить цвет каждой фишки